Radio 4’s Today programme and at least two newspapers, the Daily Telegraph and the Daily Mail, reported news earlier this week from the Institute of Psychiatry in London of a “fast, accurate” test for Alzheimer’s Disease, using a software programme to analyse brain scans.
 
The press release and the reports said that the test can return “85 per cent accuracy” in under 24 hours. But what does this mean?
 
With a diagnostic test, three aspects are important:

• The proportion of actual cases whom the test fails to diagnose (false negative rate)
• The proportion of non-cases whom the test falsely labels ‘case’ (false positive rate)
• And the mix of cases and non-cases who attend the memory clinic, because the proportion of all attendees who are correctly identified by the diagnostic test as case/non-case depends on this, too.

So in the absence of fuller information, it is impossible to interpret what 85 per cent accuracy actually means.
 
Suppose that, out of 1,000 patients who attend a memory clinic for early diagnosis of Alzheimers disease, only 150 actually have AD. At no investigative cost whatsoever, I’d get 85 per cent of my labelling right if I simply cancelled the clinic and told everyone that they had nothing to worry about. However, my false negative rate would be dire at 100 per cent of cases mislabelled.
 
Two examples show that a test that wasn’t very good could nonetheless claim “85 per cent accuracy” depending on how the mathematics was done. Suppose that the false negative rate was 44 per cent and the false positive rate was 10 per cent, then I’d expect the following in a clinic in which 15 per cent of those attending were actually suffering early AD.
 
        
 
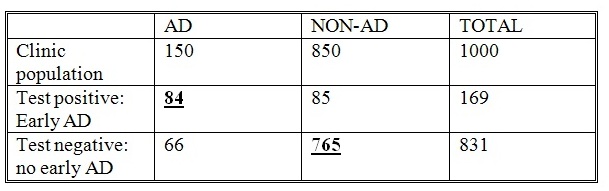
The top line represents the population attending the clinic: of 1,000 patients 150 have AD and 850 do not. If the false negative rate is 44 per cent, 66 of the actual AD patients are misdiagnosed as not having the disease, while 84 are correctly diagnosed as having it. If the false positive rate is 10 per cent, then 85 of those without AD are misdiagnosed as having it, while 765 are correctly diagnosed as not having it.
 
The total number correctly diagnosed is made up of the numbers in bold and underlined , 84 + 765 = 849 – that is, almost 85 per cent. But only half of the 169 patients told they had early symptoms of AD would actually be cases.
 
Let’s now change the case mix so that half of the patients who attend the memory clinic are actual AD cases, and half are not. The false positive and false negative rates remain the same as before. 
 
    
 
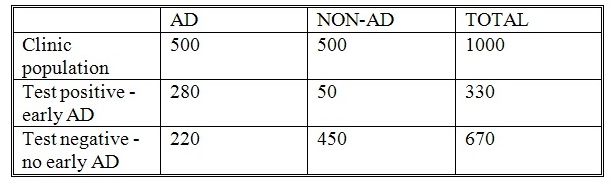
In this case, the test identifies 330 cases of early-AD, of which 85 per cent (280) are correct diagnoses.  Is this what is meant by 85 per cent accuracy?
 
If so, it would mean that 220 clinic attenders would be told that they did not have AD, when in fact they did and 50 told they had it when they didn’t – hardly an impressive result. Yet it might still be claimed by some that the test was 85 per cent accurate.
 
These illustrations show that “85 per cent accuracy” is a meaningless claim without further information.